搜索结果: 1-15 共查到“椭圆型偏微分方程”相关记录171条 . 查询时间(3.906 秒)
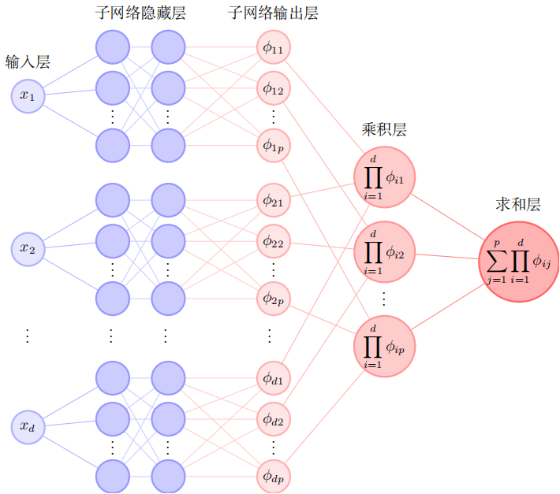
由于“维数灾难”的原因,求解高维偏微分方程一直是数学、物理、化学等学科中具有本质困难的问题。基于深度神经网络的机器学习方法为解决这一问题提供了潜在的可能性,目前已经设计了多种机器学习方法来求解高维偏微分方程。这些方法由于需要进行采样或使用Monte-Carlo方法进行高维积分来计算损失函数,往往导致求解精度远低于经典算法求解低维偏微分方程的精度,实际应用范围也受到了很大的限制。
Academy of Mathematics and Systems Science, CAS Colloquia & Seminars:"Inverse problems for elliptic PDE" (7)
椭圆偏微分方程 反问题 Calderón问题
2023/11/29
Academy of Mathematics and Systems Science, CAS Colloquia & Seminars:"Inverse problems for elliptic PDE" (8)
椭圆偏微分方程 反问题 Calderón问题
2023/11/29
对称椭圆特征值问题的一个局部化的最优预处理Newton-Schur方法
对称椭圆 特征值问题 局部化 最优预处理 Newton-Schur
2023/12/13
非自伴Dirac算子的椭圆有限带位势
非自伴 Dirac算子 椭圆 有限带位势
2023/12/13
Academy of Mathematics and Systems Science, CAS Colloquia & Seminars:Structured Matrices Approach for Legendre Pairs
勒让德对 结构化 矩阵方法
2023/4/17
Academy of Mathematics and Systems Science, CAS Colloquia & Seminars:Some recent progress on the gradient estimates for the insulated conductivity problem
绝缘 电导率 梯度估计 椭圆偏微分方程
2023/4/17
Academy of Mathematics and Systems Science, CAS Colloquia & Seminars:Pseudorandomness of Sato-Tate Distributions for Elliptic Curves
椭圆曲线 佐藤-泰特分布 伪随机性
2023/4/13
Academy of Mathematics and Systems Science, CAS Colloquia & Seminars:椭圆型偏微分方程有关的正则性问题
椭圆型 偏微分方程 正则性问题
2023/4/13
Academy of Mathematics and Systems Science, CAS Colloquia & Seminars:椭圆型偏微分方程有关的正则性问题 椭圆型偏微分方程有关的正则性问题
椭圆型偏微分方程 正则性问题 Calderon-Zygmund估计 Schauder估计
2023/4/18
Academy of Mathematics and Systems Science, CAS Colloquia & Seminars:A Liouville’s theorem for some Monge-Ampère type equations
蒙日-安培型方程 刘维尔定理 单调准局部质量类型量
2023/4/13
Academy of Mathematics and Systems Science, CAS Colloquia & Seminars:Twisted Real quasi-elliptic cohomology
扭曲 实拟椭圆 上同调
2023/4/13
Academy of Mathematics and Systems Science, CAS Colloquia & Seminars:Two Approaches towards elliptic cohomology
椭圆 上同调 两种方法
2023/4/14
Academy of Mathematics and Systems Science, CAS Colloquia & Seminars:A posteriori error estimate for a WG method of H(curl)-elliptic problems
H(卷曲) 椭圆问题 WG方法 后验误差估计
2023/4/23
Academy of Mathematics and Systems Science, CAS Colloquia & Seminars:Non-local operators with low-order singular kernels
低阶 奇异内核 非局部 运算符 正则性估计 二阶椭圆方程
2023/4/24


